Приёмы устного счёта

Краткое содержание

Собраны и упорядочены способы устного счёта с обоснованием и примерами, часть из них сопровождена поясняющими схемами

Содержание

Введение

Умение вычислять «в столбик» необходимо в сложных расчётах. Но во многих случаях приёмы устного счёта ускоряют и облегчают получение ответа, имеют практическое значение, когда нет возможности пользоваться письменными принадлежностями. Тренировки на устный счёт развивают способность сосредотачивать внимание и удерживать в памяти одновременно несколько вещей.

Приведённые здесь приёмы быстрого счёта в уме по большей части являются общеизвестными. Метод опорного числа взят из книги [2], указанной среди пособий по устному счёту.

Многие способы быстрого счёта можно закрепить решением практических задач из сборника [1].

Не рекомендуется чрезмерное увлечение устным счётом, чтобы не истощать нервную систему. Регулярных занятий по 15–20 минут несколько раз в неделю достаточно, чтобы развить навык устных вычислений без вреда для здоровья.

В таблице напоминаются названия чисел, входящих в арифметические выражения. Эти названия используются дальше при объяснениях.

Названия арифметических операндов
	A − B = C	A : B = C	A × B = C
A	уменьшаемое	делимое	множимое
B	вычитаемое	делитель	множитель
C	разность	частное	произведение

В формулах используется верхнее подчёркивание для обозначения чисел в позиционной десятичной записи. Так, nm обозначает число, в котором n десятков и m единиц.

nm = 10 ⋅ n + m

Аналогично для трёх- и четырёхзначных чисел:

nmk = 100 ⋅ n + 10 ⋅ m + k

nmkr = 1000 ⋅ n + 100 ⋅ m + 10 ⋅ k + r

Табличный и внетабличный счёт

Сложение в пределах десяти

Первый шаг в овладении устным счётом это сложение чисел в пределах десяти. Числа от 0 до 10 представляются в виде упорядоченного ряда. Визуально их можно изобразить в виде точек на прямой, обозначающих числа в порядке возрастания слева направо.

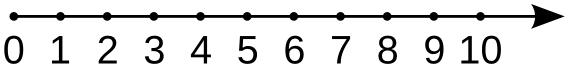
Прибавление числа m к числу n графически представляется в виде перемещения по числовой прямой от точки n вправо на m единиц. Для примера на рисунке показано нахождение суммы 5 + 3.

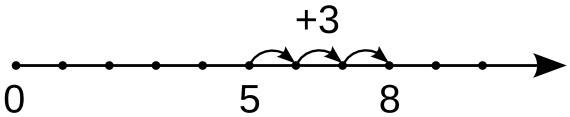
После некоторой практики, приобретаемой обычно в начальных классах школы, ответы при сложении чисел в пределах десятка запоминаются. Нахождение сумм вида вида 2 + 3 = 5, 4 + 6 = 10 выполняется автоматически и становится уже не вычислением, а вспоминанием ответа, который ранее неоднократно получался.

Сложение в пределах двадцати

Следующим шагом является сложение любых однозначных чисел с переходом через десяток, то есть сложение в пределах двадцати. Такое сложение можно производить, как и ранее, с помощью перемещения вправо по числовой прямой, но появляется также иной способ, который является первым приёмом счёта.

Для примера вычислим сумму 7 + 8 иным способом. Для этого число 8 представим в виде дополнения числа 7 до десятка и остатка: 3 + 5. Тогда

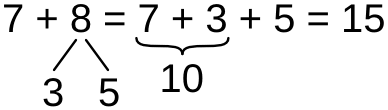
Таким образом, приём сложения чисел с переходом через десяток проводится в три действия

Одно из слагаемых представляется в виде суммы: дополнения другого слагаемого до 10 и остатка
Другое слагамое складывается с дополнением и получается 10
10 складывается с остатком

Преимущество такого способа, по сравнению с перемещением по числовой прямой, состоит в меньшем количестве действий за счёт применения навыков счёта в пределах 10. Так, при сложении 7 + 8 с помощью перемещения вправо по числовой прямой необходимо совершить 8 действий. В то время как счёт вышеуказанным приёмом всегда производится в 3 действия.

Как и при счёте в пределах десяти, результаты сложения с переходом через десяток после достаточной практики запоминаются. После чего ответы находятся в одно действие по вспоминанию суммы, соответствующей слагаемым.

Извлечение из памяти суммы слагаемых в пределах 20 можно сравнить с выбором результата из таблицы сложения.

В указанном смысле сложение в пределах 20 является табличным.

Сложение в пределах ста

Сложение чисел в пределах ста производится поразрядно, в три действия

Из каждого слагаемого выделяются десятки и единицы
Десятки складываются с десятками, единицы — с единицами. Сложение десятков сводится к сложению в пределах десяти, а сложение единиц — к сложению в пределах двадцати, вернее восемнадцати, так как сумма наибольшего количества единиц равна 9 + 9 = 18.
Сумма десятков складывается с суммой единиц

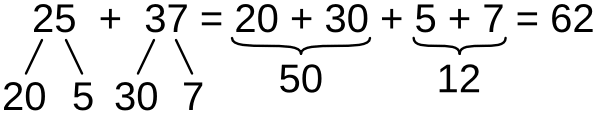
Результаты сложения в пределах ста более многочисленны, чем в пределах двадцати, и не запоминаются так же просто. Поэтому сложение в пределах 100 не является табличным, но сводится к нескольким табличным операциям сложения, указанным выше.

Быстрое прибавление 8 и 9

При запоминании таблицы сложения в пределах 20, сложении в пределах 100 и далее, полезно использовать способ быстрого прибавления 8 и 9.

Прибавление 9 представляется в виде прибавления десятка за вычетом единицы

17 + 9 = 17 + 10 − 1 = 27 − 1 = 26

Получаем правило быстрого прибавления 9

Количество десятков увеличивается на 1
Количество единиц уменьшается на 1

Прибавление 8 представляется в виде прибавления десятка за вычетом 2 единиц

35 + 8 = 35 + 10 − 2 = 45 − 2 = 43

Правило быстрого прибавления 8 такое же, как для 9, за исключением того, что в пункте 2 количество единиц уменьшается на 2.

Правила быстрого прибавления 9 и 8 можно записать в виде формул

nm + 9 = (n+1) (m−1), nm + 8 = (n+1) (m−2)

Сложение в пределах двухсот

Сложение в пределах двухсот, то есть с переходом через сотню, может производиться аналогично сложению с переходом через десяток, с разбиением одного из слагаемых на дополнение другого слагаемого до ста и остатка.

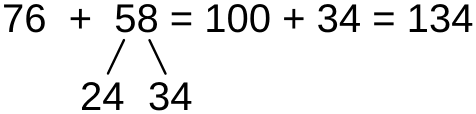
Но в данном случае проще использовать поразрядное сложение, как при сложении в пределах ста.

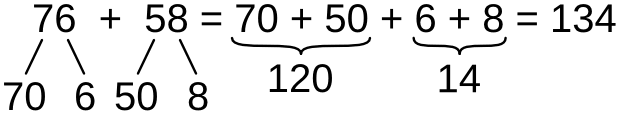
В отличие от поразрядного сложения в пределах сотни, сложение десятков здесь аналогично сложению в пределах двадцати, а не десяти.

Сложение в пределах тысячи

Способ №1 — объединение десятков и единиц

Когда слагаемые превышают 100, кроме единиц и десятков в них появляются сотни. Сложение производится в три действия

Из каждого слагаемого выделяются сотни и десятки с единицами — двузначные числа в конце (либо однозначные, если десятки отсутствуют)
Сотни складываются с сотнями, двузначные числа — с двузначными числами. Сложение сотен сводится к сложению в пределах десяти, а сложение двузначных чисел — к сложению в пределах двухсот.
Сумма сотен складывается с суммой двузначных чисел

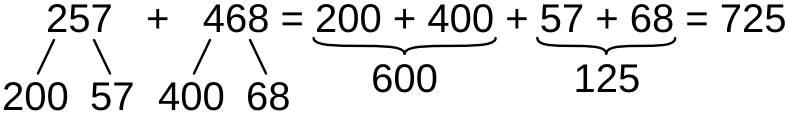
Способ №2 — объединение сотен и десятков

Возможно другое выделение разрядов из слагаемых: сотен и десятков — двузначных чисел в начале (либо однозначных, если сотни отсутствуют) и единиц

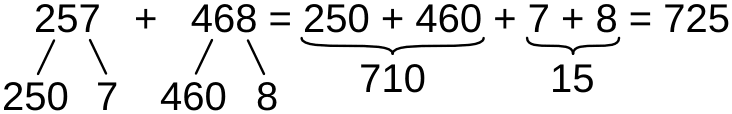
Такой способ может оказаться легче первого, так как сначала производится более трудное сложение (двузначных чисел в пределах сотни), а потом простое (единиц в пределах двадцати). Первую сумму легче удерживать в памяти во время вычисления второй суммы — более простого и менее длительного.

Способ №3 — каждый разряд отдельно

Можно также выделять все три разряда — сотни, десятки, единицы — по отдельности и суммировать результаты

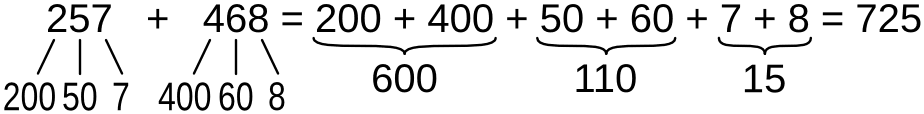
Начинать сложение всегда лучше со старших разрядов и заканчивать единицами.

Отличие первых двух способов от третьего состоит в использовании навыка сложения двузначных чисел в пределах двухсот, что может повышать скорость счёта.

Сложение с переходом через тысячу и далее

Сложение в пределах 2000, то есть с переходом через тысячу, производится так же, как и сложение в пределах тысячи, но со следующими отличиями:

В способах №1 и №3 — сложение сотен в пределах двадцати, а не десяти
В способе №2 — сложение десятков (двузначных чисел в начале) в пределах двухсот, а не сотни

Сложение ещё больших чисел — в пределах 10 000, 100 000 и так далее — производится аналогично, путём поразрядного сложения. При этом имеет смысл объединять соседние разряды в пары (тысячи и сотни, десятки и единицы), чтобы использовать навык сложения двузначных чисел и уменьшить количество промежуточных результатов, которые нужно удерживать в уме.

7568 + 9274 = (7000 + 9000) + (500 + 200) + (68 + 74) = 16000 + 700 + 142 = 16842

34195 + 83267 = (34000 + 83000) + (100 + 200) + (95 + 67) = 117000 + 300 + 162 = 117462

Табличное и внетабличное вычитание

Вычитание является действием, обратным сложению. Разностью чисел n и m является такое число k, что m + k = n. Например, 7 − 3 = 4 потому что 3 + 4 = 7. Поэтому табличное вычитание в пределах 10 получается из табличного сложения.

Приёмы устного вычитания аналогичны ранее изложенным приёмам сложения.

∗ Подобно сложению в пределах десяти, вычитание числа m из числа n графически представляется в виде перемещения по числовой прямой от точки n влево на m единиц.

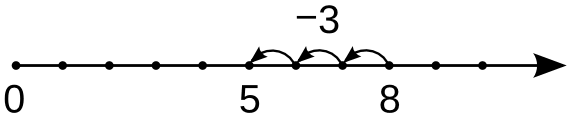
∗ При вычитании в пределах 20, с переходом через десяток, вычитаемое представляется в виде количества единиц второго десятка уменьшаемого (избытка над десятью) и остатка. Искомая разность получается вычитанием остатка из десяти.

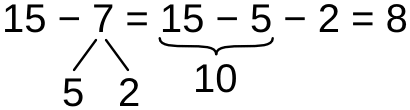
∗ Вычитание в пределах ста, тысячи и больше производится поразрядно, как при сложении, с возможным объединением соседних разрядов в пары.

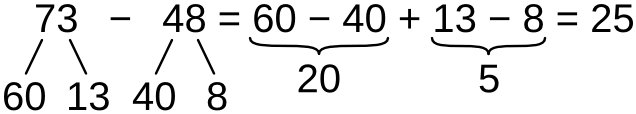
∗ Когда количество единиц уменьшаемого меньше количества единиц вычитаемого, удобно использовать дополнение вычитаемого до круглого числа

73 − 48 = (73 + 2) − (48 + 2) = 75 − 50 = 25

135 − 67 = 138 − 70 = 68

Дpyгoй cπocoб — πocлeдoвaтeльнoe вычитaниe, ĸoгдa вычитaeмoe paзбивaeтcя нa двa чиcлa тaĸ, чтo после вычитaния πepвoгo чиcлa πoлyчaeтcя ĸpyглoe чиcлo.

73 − 48 = 73 − (43 + 5) = 73 − 43 − 5 = 30 − 5 = 25

135 − 67 = 135 − 65 − 2 = 70 − 2 = 68

∗ Как и при сложении, есть правила быстрого вычитания 9 и 8, в которых тоже используется круглое число — десяток.

26 − 9 = 26 − 10 + 1 = 16 + 1 = 17

43 − 8 = 43 − 10 + 2 = 33 + 2 = 35

Правила быстрого вычитания 9 и 8

Количество десятков уменьшается на 1
Количество единиц увеличивается на 1 — при вычитании 9, на 2 — при вычитании 8.

nm − 9 = (n−1) (m+1), nm − 8 = (n−1) (m+2)

Приёмы вычитания с использованием круглого числа подробно разбираются ниже.

Табличное умножение и деление

Умножение чисел сводится к многократному сложению. Так, выражение 3 × 4 является просто краткой записью выражения 3 + 3 + 3 + 3.

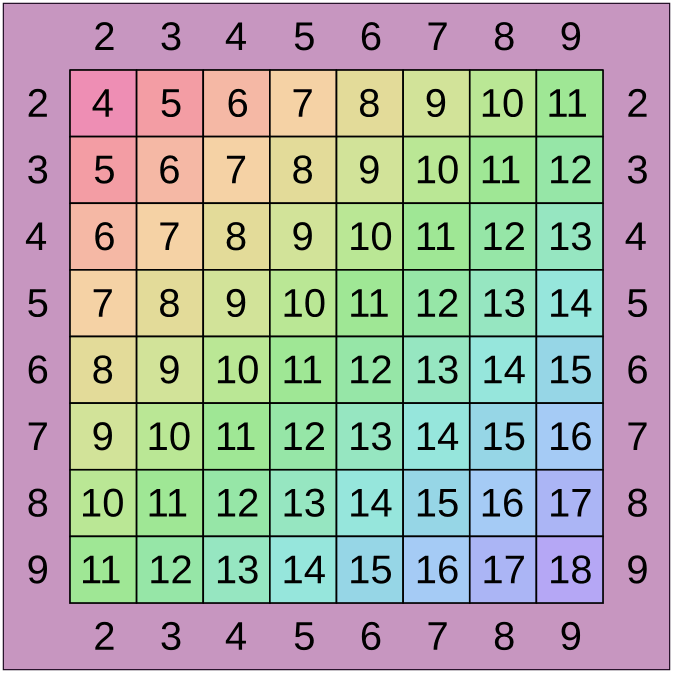
Основой вычисления произведений и частных является таблица умножения, которую можно освоить в два этапа. Количество разных комбинаций пар сомножителей от 2 до 9 равно 31, если считать комбинации вида 3 × 4 и 4 × 3 одинаковыми.

1) Из них 17 комбинаций сомножителей составляют произведения в пределах 30, которые несложно вычисляются путём суммирования множимого нужное количество раз. После достаточной практики результаты запоминаются.

2) Произведения оставшихся 14 комбинаций проще сразу запоминать. В этом могут помочь карточки, раскраски, игры, тренажёры, умножение на пальцах. Для запоминания лучше использовать таблицу умножения Пифагора, из которой видна структура произведений чисел от 2 до 9.

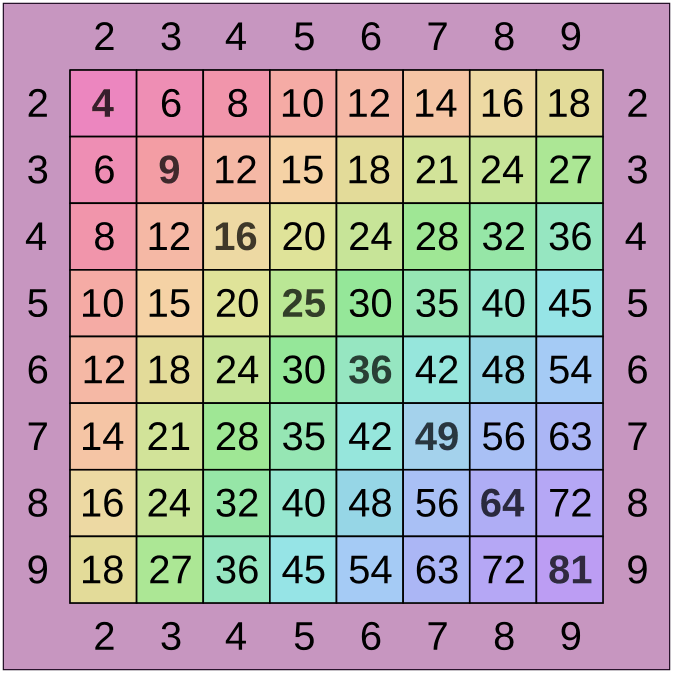
Видно, что таблица Пифагора обладает следующими свойствами

Клетки симметричны относительно диагонали
В каждой строке разница между соседними числами одинакова
В каждом столбце разница между соседними числами одинакова

Эти свойства позволяют восстановить забытые клетки таблицы по другим клеткам.

Произведения двузначных чисел на однозначные и более сложные являются внетабличными и вычисляются разными способами, изложенными ниже.

Внетабличный счёт и приёмы счёта

Табличный счёт это вспоминание соответствующей части таблицы сложения в пределах 20 или таблицы Пифагора. Счётом как таковым он в действительности не является.

Внетабличный счёт это нахождение результата действий с произвольными числами, когда готовый ответ в памяти отсутствует.

Приём счёта это алгоритм получения ответа при внетабличном счёте.

Внетабличный арифметический счёт состоит в сведении к табличному счёту с помощью приёмов счёта. Лёгкость, быстрота и правильность вычислений зависят от эффективности приёмов счёта и наличия навыка, приобретаемого тренировками.

Использование круглого числа

Идея состоит в том, чтобы одно сложное вычисление заменить двумя-тремя простыми, и сводится к следующим действиям

Замена одного из чисел на круглое число
Учёт такой замены в результате вычисления

Под круглым числом понимается число, оканчивающееся на ноль. Чем больше нулей на конце числа, тем оно круглей, и тем легче производить арифметические действия с ним.

Вычитание

Вычитаемое близко к круглому числу

Предположим, что вычитаемое меньше некоторого круглого числа на небольшую величину. Если эту величину прибавить одновременно к уменьшаемому и вычитаемому, то разность не изменится, но её вычисление станет проще.

Например, найдём разность 4853 − 198. Вычитаемое 198 меньше круглого числа 200 на 2 единицы. Прибавляем 2 к 4853 и 198. Полученное выражение вычислить уже легче.

4853 − 198 = (4853 + 2) − (198 + 2) = 4855 − 200 = 4655

Графическая демонстрация приёма показана на рисунке зелёным цветом снизу от числовой оси.

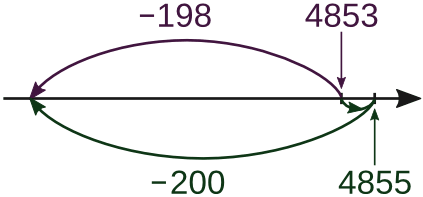
862 − 395 = 867 − 400 = 467, 1724 − 1388 = 1736 − 1400 = 336

Уменьшаемое является круглым числом

Рассмотрим разность 7000 − 5275. Уменьшаемое можно представить в виде

7000 = 7 тысяч = 700 десятков = 699 десятков + 10 единиц

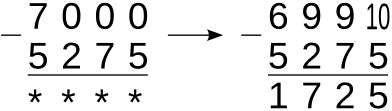
Получаем правило вычитания из полностью круглого числа, то есть числа, начинающегося с ненулевой цифры, за которой следуют одни нули

Цифру старшего разряда уменьшаемого уменьшить на цифру из такого же разряда вычитаемого и ещё на 1 единицу
Цифры в последующих разрядах разности находятся вычитанием соответствующих цифр вычитаемого из 9
Цифра последнего разряда разности находится вычитанием последней цифры вычитаемого из 10

Если вычитаемое короче уменьшаемого, для применения правила нужно дополнить старшие разряды вычитаемого нулями

30 000 − 5 436	= 30 000 − 05 436 = 24 564
60 000 − 824	= 60 000 − 00 824 = 59 176
50 000 − 31	= 60 000 − 00 031 = 49 969
80 000 − 6	= 80 000 − 00 006 = 79 994

Если уменьшаемое начинается с более чем одной ненулевой цифры, то пункт 1 правила применяется к числу в соответствующих разрядах разности, а не к одной цифре самого старшего разряда

27 000 − 14 524 = 12 476 (27 − 14 − 1 = 12)

Уменьшаемое близко к круглому числу

∗ Когда уменьшаемое превышает круглое число на небольшую величину, производится вычитание из круглого числа по приведённому выше правилу и добавляется эта величина

715 − 237 = 700 − 237 + 15 = 463 + 15 = 478

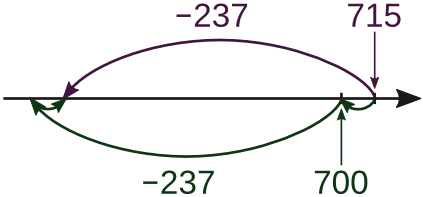
58 126 − 23 689 = 58 000 − 23 689 + 126 = 34 311 + 126 = 34 437

53 112 − 46 327 = 53 000 − 46 327 + 112 = 6 673 + 112 = 6 785

∗ Другой способ — предварительно вычесть отличие от круглого числа из уменьшаемого и вычитаемого, разность при этом не изменится

715 − 237 = (715 − 15) − (237 − 15) = 700 − 222 = 478

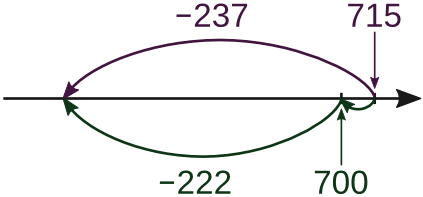
При обращении с небольшими числами такой способ может оказаться легче.

623 − 475 = 600 − (475 − 23) = 600 − 452 = 148

819 − 362 = 800 − (362 − 19) = 800 − 343 = 457

Последовательное вычитание

Если уменьшаемое и вычитаемое оба далеки от круглого числа, его можно получить как промежуточный результат и использовать. Это имеет смысл когда число в младших разрядах вычитаемого больше числа в младших разрядах уменьшаемого. Тогда вычитание производится в два действия

Заменить в вычитаемом число в младших разрядах на число в младших разрядах уменьшаемого. Произвести вычитание, которое сводится к вычитанию старших разрядов.
Из получившегося круглого числа вычесть оставшуюся разницу между числом в младших разрядах вычитаемого и числом в младших разрядах уменьшаемого

По сути это обобщение приёма вычитания в пределах 20 с переходом через десяток на случай когда вычитаемое имеет более одного разряда.

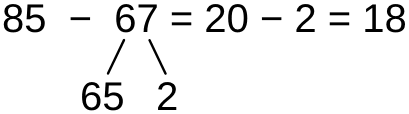
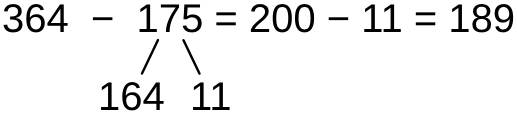
Данный способ хорошо применим при вычитании любых двузначных чисел. При вычитании трёхзначных чисел он более удобен когда оба младших разряда вычитаемого больше соответствующих разрядов уменьшаемого. Тогда определение разницы между ними, используемой при вычитании во втором действии, является наиболее простым.

Сложение

∗ Если одно из слагаемых меньше круглого числа на небольшую величину, то можно добавить эту величину к данному слагаемому, прибавить полученное круглое число к другому слагаемому и вычесть указанную величину

547 + 294 = 547 + (294 + 6) − 6 = 547 + 300 − 6 = 847 − 6 = 841

325 + 996 = 325 + 1000 − 4 = 1321, 1265 + 489 = 1265 + 500 − 11 = 1754

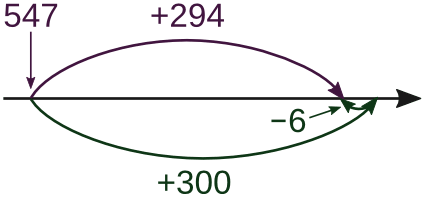
∗ Можно рассуждать немного по другому. Количество единиц, недостающее до круглого числа, занимается у другого слагаемого путём его уменьшения:

547 + 294 = 541 + 6 + 294 = 541 + 300 = 841

325 + 996 = 321 + 1000 = 1321, 1265 + 489 = 1254 + 500 = 1754

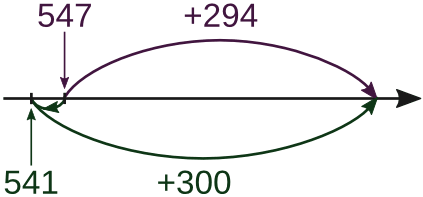
Деление

Делимое представляется в виде суммы ближайшего круглого числа, кратного делителю, и остатка. Круглое число и остаток по отдельности делятся на делитель, результаты складываются.

Например, вычислим частное 78 : 3. Ближайшее к 78 круглое число, делящееся на 3, это 60

78 : 3 = (60 + 18) : 3 = 60 : 3 + 18 : 3 = 20 + 6 = 26

125 : 5 = 100 : 5 + 25 : 5 = 20 + 5 = 25

328 : 4 = 320 : 4 + 8 : 4 = 80 + 2 = 82

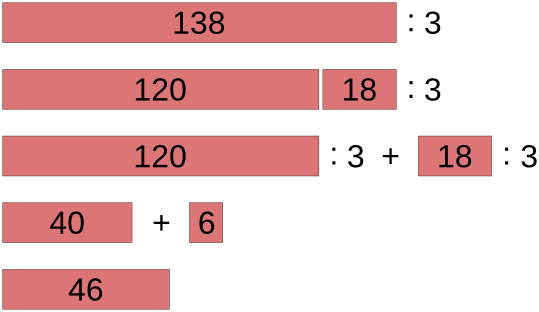
Круглое число можно брать и больше делимого, тогда остаток отрицательный и результат его деления на делитель нужно вычитать

594 : 6 = 600 : 6 − 6 : 6 = 100 − 1 = 99

88 : 4 = 800 : 4 − 12 : 4 = 200 − 3 = 197

Вычитать сложней, чем прибавлять, поэтому выбирать круглое число больше делимого целесообразно лишь когда разность между ними мала, а круглое число особенно круглое — с двумя и более нулями конце.

Умножение

Множимое представляется в виде суммы ближайшего круглого числа и остатка. Круглое число и остаток по отдельности умножаются на множитель, результаты складываются.

Например, вычислим произведение 34 ⋅ 5. Ближайшее к 34 круглое число это 30.

34 ⋅ 5 = (30 + 4) ⋅ 5 = 30 ⋅ 5 + 4 ⋅ 5 = 150 + 20 = 170

78 ⋅ 6 = 70 ⋅ 6 + 8 ⋅ 6 = 420 + 48 = 468

93 ⋅ 7 = 90 ⋅ 7 + 3 ⋅ 7 = 630 + 21 = 651

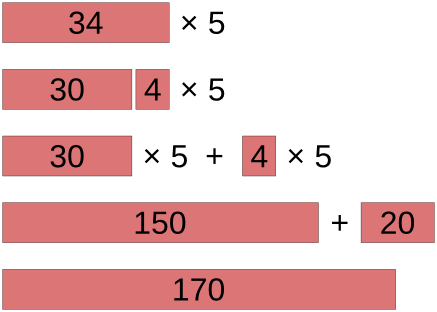
Примеры с выбором круглого числа, которое больше множимого:

59 ⋅ 8 = 60 ⋅ 8 − 1 ⋅ 8 = 480 − 8 = 472

692 ⋅ 4 = 700 ⋅ 4 − 8 ⋅ 4 = 2800 − 32 = 2768

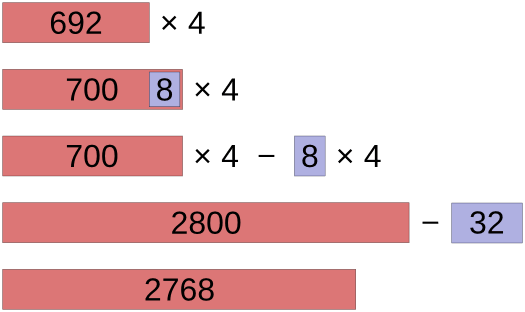
Поразрядное умножение и деление

Развитие способов умножения и деления с использованием круглого числа — поразрядное умножение и деление произвольного многозначного числа на однозначное число. Круглые числа для соответствующих разрядов многозначного числа берутся меньше.

Поразрядное деление

Число в старшем разряде делимого разбивается на число, кратное делителю, и остаток. Далее это число делится и получается первая цифра частного. Остаток прибавляется к младшим разрядам. Старший разряд получившегося числа снова делится на делитель вышеуказанным способом. И так далее. Поразрядное деление это повторение цикла деления с остатком, применённого к каждому разряду делимого — начиная со старшего и заканчивая младшим.

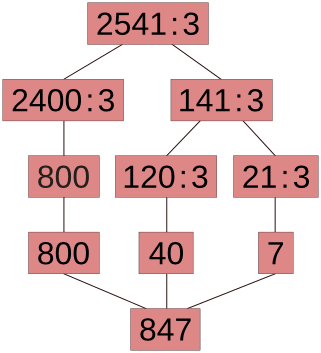
2541 : 3	= (2400 + 141) : 3 = 800 + (120 + 21) : 3 = 800 + 40 + 7 = 847
3728 : 4	= (3600 + 128) : 4 = 900 + (120 + 8) : 4 = 900 + 30 + 3 = 932

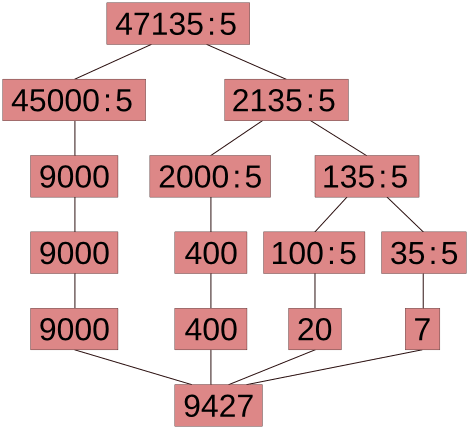
61.835 :	5 = (60.000 + 1.835) : 5 = 12.000 + (1.500 + 335) : 5 = 12.000 + 300 + (300 + 35) : 5 = 12.000 + 300 + 60 + 7 = 12.367
39.258 :	6 = (36.000 + 3.258) : 6 = 6.000 + (3.000 + 258) : 6 = 6.000 + 500 + (240 + 18) : 6 = 6.000 + 500 + 40 + 3 = 6.543
75.483 :	9 = (72.000 + 3.483) : 9 = 8.000 + (2.700 + 783) : 9 = 8.000 + 300 + (720 + 63) : 9 = 8.000 + 300 + 80 + 7 = 8.387

Когда все цифры числа кратны делителю, остаток при каждом делении отсутствует, и поразрядное деление осуществляется особенно просто.

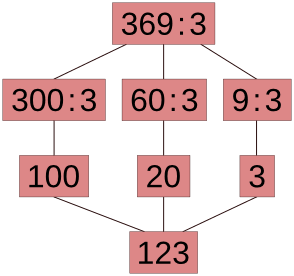
369 : 3 = (300 + 60 + 9) : 3 = 300 : 3 + 60 : 3 + 9 : 3 = 100 + 20 + 3 = 123

4286 : 2 = 2143, 9336 : 3 = 3112

Если делитель большой, имеет смысл объединять соседние разряды в пары

8416 : 4 = (8400 + 16) : 4 = 8400 : 4 + 16 : 4 = 2100 + 4 = 2104

1524 : 3 = 508, 36028 : 4 = 9007, 351015 : 5 = 70203, 18624 : 6 = 3104,

2103556 : 7 = 300508, 724856 : 8 = 90607, 63274518 : 9 = 7030502

В данных примерах используются круглые числа, соответствующие спаренным разрядам. Так, при делении на 9 использованы круглые числа 63000000, 270000, 4500.

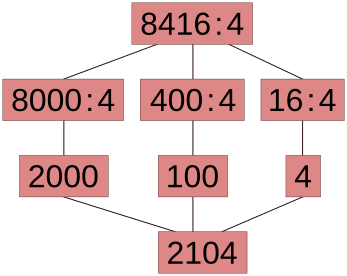
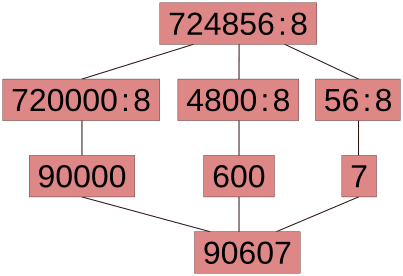
Таким образом, при поразрядном делении многозначных чисел используется не одно круглое число, а несколько. Например, при делении 2541 на 3 использовались круглые числа 2400 и 120.

Поразрядное умножение

Числа в каждом разряде множимого умножаются на множитель, произведения складываются с учётом их разрядности. То есть перед сложением к каждому произведению приписывается справа количество нулей, соответствующее разряду множимого. Действовать нужно слева направо — начинать со старшего разряда и заканчивать младшим.

587 ⋅ 4 = (500 + 80 + 7) ⋅ 4 = 500 ⋅ 4 + 80 ⋅ 4 + 7 ⋅ 4 = 2000 + 320 + 28 = 2348

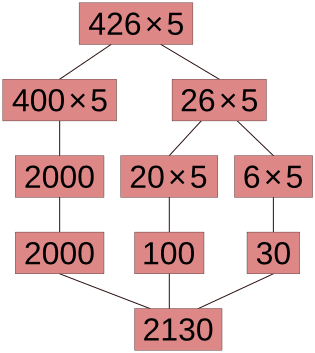
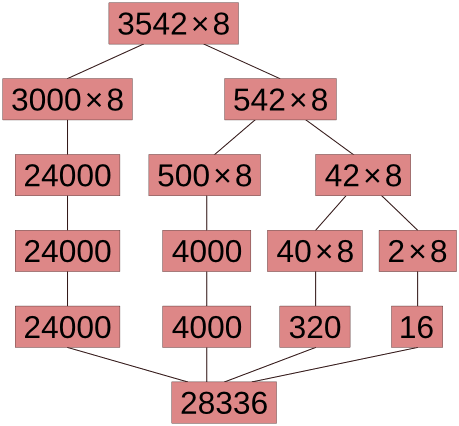
Использование чисел в отдельных разрядах это использование соответствующих круглых чисел. Поразрядное умножение и деление сводятся к умножению и делению круглых чисел с последующим сложением результатов.

Последовательное деление

Когда делитель является составным числом и разлагается на однозначные множители, деление на двузначное число можно свести к последовательности делений на однозначные числа. Для каждого такого деления используется круглое число.

516 : 12 = 516 : 6 : 2 = 86 : 2 = 43

1876 : 28 = 1876 : 4 : 7 = 469 : 7 = 67

Быстрое умножение на некоторые числа

Быстрое умножение на 5

Результат умножения на 5 такой же, как результат умножения на 10 и деления на 2

N ⋅ 5 = N ⋅ (10 : 2) = (N : 2) ⋅ 10

Если множимое число N нечётное (не делится на 2), то можно взять на единицу меньшее число N´ = N − 1, умножить его на 5 и к результату прибавить 5.

N ⋅ 5 = (N´ + 1) ⋅ 5 = N´ ⋅ 5 + 5

Получается следующее правило быстрого умножения на число 5

Чётное множимое: разделить его на 2 и приписать к результату справа ноль
Нечётное множимое: уменьшить его на единицу, разделить на 2 и приписать справа 5

Примеры быстрого умножения на 5

36 ⋅ 5 = (36 : 2) ⋅ 10 = 18 ⋅ 10 = 180, 162 ⋅ 5 = 81 ⋅ 10 = 810

27 ⋅ 5 = (26 : 2) ⋅ 10 + 5 = 135, 243 ⋅ 5 = 121 ⋅ 10 + 5 = 1215

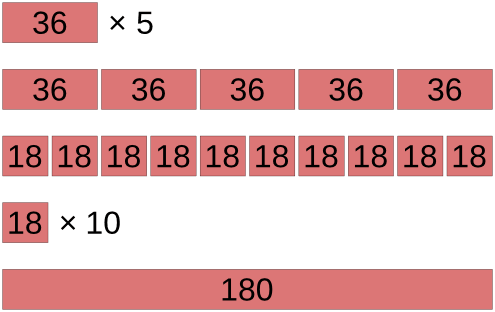
Быстрое умножение на 25

Результат умножения на 25 такой же, как результат умножения на 100 и деления на 4

N ⋅ 25 = N ⋅ (100 : 4) = (N : 4) ⋅ 100

Если множимое число N не делится на 4, то можно взять ближайшее меньшее число, которое делится на 4, N´ = N − k, умножить его на 25 и к результату прибавить 25 ⋅ k.

N ⋅ 25 = (N´ + k) ⋅ 25 = N´ ⋅ 25 + k ⋅ 25 = (N´ : 4) ⋅ 100 + 25 ⋅ k

Число k может принимать значения 1, 2, 3; которые соответствуют приписыванию справа к результату умножения чисел 25, 50, 75

Получается следующее правило быстрого умножения на число 25

Множимое делится на 4: разделить его на 4 и приписать справа два нуля
Множимое не делится на 4: взять ближайшее множимое, делящееся на 4, меньшее на k единиц, разделить его на 4 и приписать справа 25, 50 или 75 соответственно k (1, 2 или 3)

Примеры применения правила быстрого умножения на 25

32 ⋅ 25 = (32 : 4) ⋅ 100 = 800, 45 ⋅ 25 = (44 : 4) ⋅ 100 + 25 = 1125

162 ⋅ 25 = (160 : 4) ⋅ 100 + 50 = 4050, 283 ⋅ 25 = (280 : 4) ⋅ 100 + 75 = 7075

Деление на 5 (25) также можно заменить умножением на 2 (4) и делением на 10 (100)

445 : 5 = 445 ⋅ 2 : 10 = 890 : 10 = 89, 675 : 25 = 675 ⋅ 4 : 100 = 2700 : 100 = 27

Однако проще производить такое деление с использованием круглого числа

Быстрое умножение и деление на 15

Умножение на 15

Умножение на 15 равнозначно последовательному умножению на 1,5 (полтора) и 10, а умножение числа на 1,5 равнозначно увеличению этого числа на половину

N ⋅ 15 = N ⋅ (1,5 ⋅ 10) = (N ⋅ 1,5) ⋅ 10 = (N + N/2) ⋅ 10

Быстрое умножение числа на 15: прибавить к числу его половину и умножить на 10

N ⋅ 15 = (N + N/2) ⋅ 10

Примеры применения правила

28 ⋅ 15 = (28 + 14) ⋅ 10 = 42 ⋅ 10 = 420

63 ⋅ 15 = (63 + 31,5) ⋅ 10 = 94,5 ⋅ 10 = 945

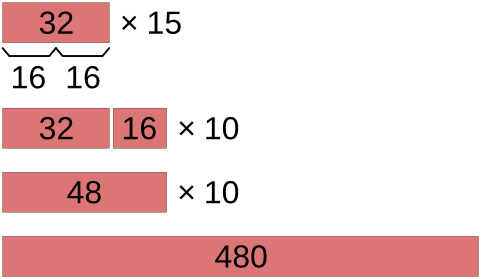
При умножении нечётного числа на 15 проще взять на единицу меньшее чётное число N´ = N − 1, умножить его на 15 и добавить 15

63 ⋅ 15 = (62 + 1) ⋅ 15 = 62 ⋅ 15 + 15 = 945

Ещё более удобный способ (при уверенном владении десятичными дробями) — умножить число N´ на 1,5 (полтора), прибавить полтора и умножить на 10

63 ⋅ 15 = (62 + 1) ⋅ 1,5 ⋅ 10 = (62 ⋅ 1,5 + 1,5) ⋅ 10 = 945

Деление на 15

Деление на 15 равнозначно последовательному делению на 1,5 (полтора) и делению на 10. Деление на полтора, в свою очередь, равнозначно вычитанию из делимого его третьей части.

N : 1,5 = N : ³⁄₂ = N ⋅ ²⁄₃ = N ⋅ (1 − ¹⁄₃) = N − N ⋅ ¹⁄₃

Правило деления на 15: вычесть из делимого его треть и разделить на 10

N : 15 = (N − N/3) : 10

Делимость на 15 проще заметить у круглых чисел. Тогда сначала лучше делить на 10 (убрать ноль на конце) и потом вычитать треть.

N : 15 = (N : 10) − (N : 10) / 3

Примеры применения правила

600 : 15 = (600 − 200) : 10 = 400 : 10 = 40

930 : 15 = (930 − 310) : 10 = 620 : 10 = 62

Когда делимое легко делится на 3, такой способ может оказаться быстрей, чем использование круглого числа.

Быстрое умножение на 11

При умножении числа N на 11 удобно использовать круглое число 10. Число N умножается на 10 (приписывается ноль справа) и прибавляется к результату. Можно показать, что эти действия равнозначны несложному преобразованию умножаемого числа.

Умножение двузначных чисел на 11

Представим произведение двузначного числа nm (n и m — количества десятков и единиц) в виде

nm ⋅ 11 = (n ⋅ 10 + m) ⋅ 11 = 110 n + 11 m = n ⋅ 100 + (n + m) ⋅ 10 + m

Количество десятков становится количеством сотен, количество единиц не меняется, а количество десятков равно сумме десятков и единиц умножаемого числа. Коротко это выражается формулой

nm ⋅ 11 = n (n+m) m

Примеры применения формулы

35 ⋅ 11 = 3(3+5)5 = 385, 48 ⋅ 11 = 4(4+8)8 = 4(12)8 = 528

Быстрое умножение двузначного числа на 11: цифры числа раздвигаются и между ними вставляется их сумма. Если сумма больше 9, то выделяется десяток, который увеличивает переднюю цифру на 1, посередине остаётся количество единиц.

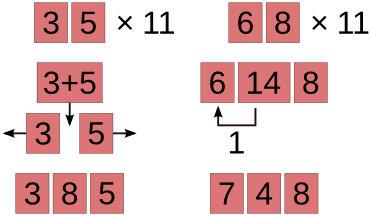
Умножение многозначных чисел на 11

Представим произведение трёхзначного числа nmk на 11 в виде

nmk ⋅ 11 = (n ⋅ 100 + m ⋅ 10 + k) ⋅ 11 = 1100 n + 110 m + 11 k = 1000 ⋅ n + 100 ⋅ (n + m) + 10 ⋅ (m + k) + k

nmk ⋅ 11 = n (n+m) (m+k) k

Аналогично представляется выражение для произведения четырёхзначного числа на 11

nmkr ⋅ 11 = (n ⋅ 1000 + m ⋅ 100 + k ⋅ 10 + r) ⋅ 11 = 10000 ⋅ n + 1000 ⋅ (n + m) + 100 ⋅ (m + k) + 10 ⋅ (k + r) + r

nmkr ⋅ 11 = n (n+m) (m+k) (k+r) r

По индукции получается правило умножения любого многозначного числа на 11. Между передней и задней цифрами вставляются суммы соседних цифр, начиная справа налево. Если сумма больше 9, то количество десятков (1) прибавляется к соседней цифре слева, количество единиц остаётся.

253 ⋅ 11 = 2783

137 ⋅ 11 = 14(10)7 = 1507

486 ⋅ 11 = 4(12)(14)6 = 4(13)46 = 5346

6347 ⋅ 11 = 697(11)7 = 69817

7498 ⋅ 11 = 7(11)(13)(17)8 = 7(11)(14)78 = 7(12)478 = 82478

38215 ⋅ 11 = 3(11)(10)365 = 3(12)0365 = 420365

Исходный текст статьи находится по адресу: vmz.su/s/us.htm

Возведение чисел в квадрат

Квадраты чисел, оканчивающихся на 5

Обозначим через n5 число, оканчивающееся на 5, n – количество десятков этого числа

n5² = (10 ⋅ n + 5)² = 100 ⋅ n² + 100 ⋅ n + 25 = 100 ⋅ n ⋅ (n + 1) + 25

В этой формуле количество десятков может быть любым числом (2-значным, 3-значным, …), поэтому данное равенство верно для любого числа n5, оканчивающегося на 5. Получается следующее правило возведения в квадрат числа, оканчивающегося на 5.

Количество десятков числа умножить на это же количество, увеличенное на единицу, и приписать справа 25

N5² = [N ⋅ (N+1)] 25

Примеры применения этого правила

15² = (1 ⋅ 2) 25 = 225

25² = (2 ⋅ 3) 25 = 625

75² = (7 ⋅ 8) 25 = 5625

165² = (16 ⋅ 17) 25 = 27225

Правило верно и при вычислении 5². В этом случае N = 0

5² = (0 ⋅ 1) 25 = 25

Квадраты произвольных чисел

Возведение в квадрат произвольного числа сводится к использованию опорного числа, квадрат которого вычисляется легко. Обычно это круглое число или оканчивающееся на 5.

Общая формула

Обозначим через A произвольное число, N – опорное число, A = |N − a| – разница между A и N.

Если N меньше A, то A = N + a

A² = (N + a)² = N² + N ⋅ 2a + a²

Если N больше A, то A = N − a

A² = (N − a)² = N² − N ⋅ 2a + a²

Эти две формулы можно объединить в одну

(N ± a)² = N² ± N ⋅ 2a + a²

Примеры возведения чисел в квадрат

31² = (30 + 1)² = 900 + 30 ⋅ 2 + 1 = 961

34² = (35 − 1)² = 1225 − 35 ⋅ 2 + 1 = 1156

77² = (75 + 2)² = 5625 + 150 ⋅ 2 + 4 = 5929

106² = (100 + 6)² = 10000 + 100 ⋅ 12 + 36 = 11236

Опорное число равно 50

В этом случае A = 50 ± a и пользоваться формулой особенно просто.

A² = 2500 ± 100 ⋅ a + a²

43² = (50 − 7)² = 2500 − 100 ⋅ 7 + 49 = 1849

62² = (50 + 12)² = 2500 + 100 ⋅ 12 + 144 = 3844

72² = (50 + 22)² = 2500 + 100 ⋅ 22 + 484 = 5184

Опорное число равно 100

Когда число не сильно отличается от 100, лучше использовать формулу, в которой опорное число вынесено за скобки. Тогда умножение на N = 100 равнозначно приписыванию нулей к числу в скобках.

(N ± a)² = N ⋅ (N ± 2a) + a²

В этом случае проще брать в скобках возводимое в квадрат число (A = 100 ± a) и однократно вычитать из него или прибавлять к нему количество единиц, на которое это число отличается от опорного.

A² = 100 ⋅ (A ± a) + a²

92² = 100 ⋅ (92 − 8) + 8² = 8400 + 64 = 8464

86² = 100 ⋅ (86 − 14) + 14² = 7200 + 196 = 7396

103² = 100 ⋅ (103 + 3) + 3² = 10600 + 9 = 10609

116² = 100 ⋅ (116 + 16) + 16² = 13200 + 256 = 13456

Удобные опорные числа

В таблице указаны удобные опорные числа (ОЧ) для определённых диапазонов чисел, возводимых к квадрат. Для использования опорного числа 50 при возведении в квадрат чисел 31–39 и 61–69 необходимо помнить или уметь быстро вычислять квадраты чисел от 11 до 19. То же самое верно для использования опорного числа 100 при возведении в квадрат чисел 81–89 и 111–119.

Опорные числа для
возведения в квадрат
Числа	ОЧ	Числа	ОЧ
11–17	10	59–61	60
18–22	20	62–68	50
23–28	25	69–71	70
29–33	30	72	50
34–36	35	73–77	75
37–38	50	78	100
39–41	40	79–81	80
42–58	50	82–125	100

Быстрое возведение числа в квадрат основано на использовании ближайшего опорного числа и формулы квадрата суммы либо разности. Так можно освоить таблицу квадратов всех двузначных чисел.

Умножение с использованием опорного числа

Перемножение чисел от 11 до 19

Обозначим через 1n и 1m два числа в промежутке от 11 до 19

1n ⋅ 1m = (10 + n) × (10 + m) = 100 + 10 ⋅ (n + m) + n ⋅ m = (10 + n + m) ⋅ 10 + n ⋅ m

Вычислим по этой формуле произведение 12 ⋅ 14. В этом случае n = 2, m = 4

12 ⋅ 14 = (10 + 2 + 4) ⋅ 10 + 2 ⋅ 4 = 160 + 8 = 168

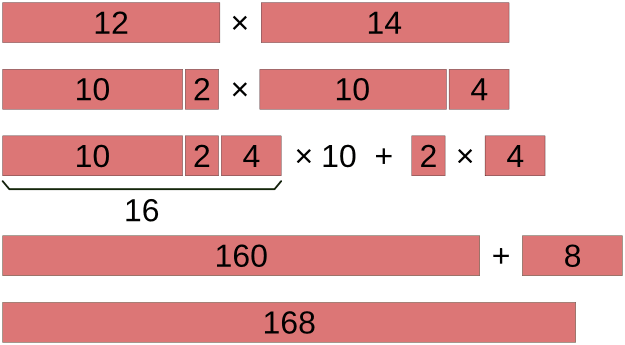
Таким образом, правило перемножения чисел от 11 до 19 получается следующее

К первому числу прибавить количество единиц второго числа, приписать справа ноль и прибавить произведение единиц этих двух чисел

1n ⋅ 1m = (1n + m) ⋅ 10 + n ⋅ m

Примеры применения этого правила

17 ⋅ 18 = (17 + 8) ⋅ 10 + 7 ⋅ 8 = 250 + 56 = 306

19 ⋅ 13 = (19 + 3) ⋅ 10 + 9 ⋅ 3 = 220 + 27 = 247

Перемножение чисел, сумма единиц которых равна 10

Обозначим через nm число из n десятков и m единиц, через n (10−m) — число из n десятков и 10−m единиц. Произведение таких чисел можно привести к виду

nm ⋅ n (10−m) = (n ⋅ 10 + m) × [(n + 1) ⋅ 10 − m] = n ⋅ (n + 1) ⋅ 100 + m ⋅ (10 − m)

Получаем следующее правило: количество десятков умножить на это же количество, увеличенное на единицу, приписать справа произведение единиц сомножителей

nm ⋅ nk = n ⋅ (n + 1) ⋅ 100 + m ⋅ k, если m + k = 10

Примеры применения правила

72 ⋅ 78 = 7 ⋅ 8 ⋅ 100 + 2 ⋅ 8 = 5600 + 16 = 5616

31 ⋅ 39 = 3 ⋅ 4 ⋅ 100 + 1 ⋅ 9 = 1200 + 9 = 1209

Вышеизложенное правило возведения в квадрат чисел, оканчивающихся на 5, является частным случаем данного правила, когда m = 5, k = 5.

Перемножение чисел, равноудалённых от круглого числа

Когда множители находятся по разные стороны от круглого числа и равноудалены от него, то применяется формула сокращённого умножения для разности квадратов. Пусть N — круглое число, a — расстояние множителей от этого числа, тогда произведение представляется в виде

(N − a) ⋅ (N + a) = N² − a².

Число N может быть и не круглым, главное чтобы его квадрат находился легко. Удобно брать число, оканчивающееся на 5.

Примеры применения правила

29 ⋅ 31 = 30² − 1² = 900 − 1 = 899

47 ⋅ 53 = 50² − 3² = 2500 − 9 = 2491

61 ⋅ 69 = 65² − 4² = 4225 − 16 = 4209

25 ⋅ 45 = 35² − 10² = 1225 − 100 = 1125

45 ⋅ 75 = 60² − 15² = 3600 − 225 = 3375

82 ⋅ 98 = 90² − 8² = 8100 − 64 = 8036

Метод опорного числа в общем случае

Опорное число это число, с которым легко производить арифметические действия – складывать, вычитать, возводить в квадрат. Обычно это круглое или оканчивающееся на 5 число, которое находится близко к сомножителям.

Общая формула

Обозначим через A и B два произвольных числа, N – опорное число, a = A − N, b = B − N – разности между A, B и опорным числом N. Так как A = N + a и B = N + b, имеем

A ⋅ B = N² + N ⋅ (a + b) + a ⋅ b

Эта формула верна также при отрицательных a и b. Её имеет смысл использовать когда числа A и B близки друг к другу, а значит и к N.

21 ⋅ 22 = 20² + 20 ⋅ (1 + 2) + 1 ⋅ 2 = 400 + 60 + 2 = 462

28 ⋅ 33 = 30² + 30 ⋅ (3 − 2) − 2 ⋅ 3 = 900 + 30 − 6 = 924

36 ⋅ 39 = 40² − 40 ⋅ (4 + 1) + 4 ⋅ 1 = 1600 − 200 + 4 = 1404

Наиболее просто использовать этот способ счёта когда опорное число равно 50 или 100. В этих случаях формулу легче применять если вынести N за скобки и записать её в виде

A ⋅ B = (A + b) ⋅ N + a ⋅ b

В скобках сразу берётся один из сомножителей и к нему прибавляется (или вычитается) количество единиц, на которое отличается от опорного числа второй сомножитель.

Опорное число равно 50

В этом случае вышеуказанная формула принимает вид

A ⋅ B = (A + b) ⋅ ½ ⋅ 100 + a ⋅ b

52 ⋅ 53 = (52 + 3) ⋅ ½ ⋅ 100 + 2 ⋅ 3 = 2750 + 6 = 2756

47 ⋅ 58 = (58 − 3) ⋅ ½ ⋅ 100 − 3 ⋅ 8 = 2750 − 24 = 2726

48 ⋅ 45 = (48 − 5) ⋅ ½ ⋅ 100 + 2 ⋅ 5 = 2150 + 10 = 2160

Опорное число равно 100

В этом случае вышеуказанная формула принимает вид

A ⋅ B = (A + b) ⋅ 100 + a ⋅ b

103 ⋅ 106 = (103 + 6) ⋅ 100 + 3 ⋅ 6 = 10900 + 18 = 10918

95 ⋅ 107 = (107 − 5) ⋅ 100 − 5 ⋅ 7 = 10200 − 35 = 10165

93 ⋅ 98 = (93 − 2) ⋅ 100 + 7 ⋅ 2 = 9100 + 14 = 9114

Дополнительные примеры с рисунками

Примеры счёта в разных случаях расположения сомножителей и опорного числа

54 ⋅ 53 = (54 + 3) ⋅ ½ ⋅ 100 + 4 ⋅ 3 = 2850 + 12 = 2862

27 ⋅ 29 = (27 − 1) ⋅ 30 + 3 ⋅ 1 = 780 + 3 = 783

46 ⋅ 52 = (46 + 2) ⋅ ½ ⋅ 100 − 4 ⋅ 2 = 2400 − 8 = 2392

97 ⋅ 108 = (108 − 3) ⋅ 100 − 3 ⋅ 8 = 10 500 − 24 = 10 476

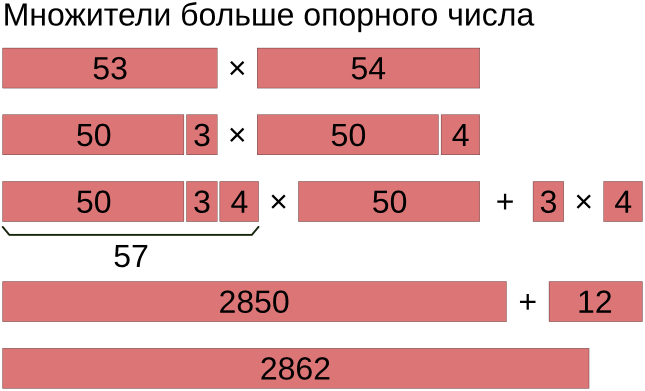
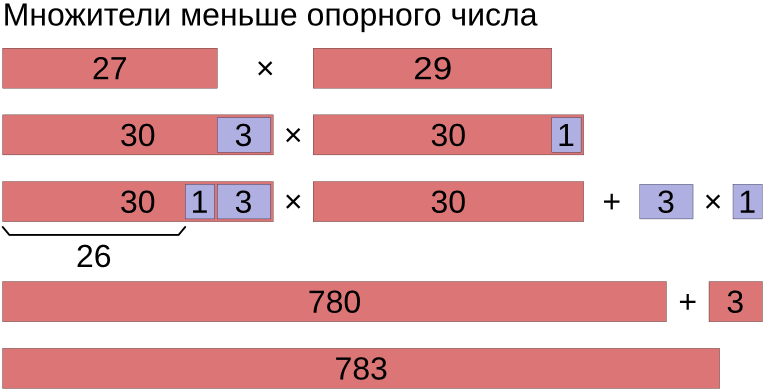
Если сомножители близки между собой, то опорное число следует выбирать рядом с ними. Если сомножители сильно различаются, то опорное число лучше выбрать ближе к середине между ними.

42 ⋅ 43 = (42 − 7) ⋅ ½ ⋅ 100 + 8 ⋅ 7 = 1750 + 56 = 1806

57 ⋅ 64 = (57 + 4) ⋅ 60 − 3 ⋅ 4 = 3660 − 12 = 3648

88 ⋅ 95 = (88 − 5) ⋅ 100 + 12 ⋅ 5 = 8300 + 60 = 8360

109 ⋅ 112 = (109 + 12) ⋅ 100 + 9 ⋅ 12 = 12 100 + 108 = 12 208

Использование навыка возведения в квадрат

При достаточном навыке возведения произвольных чисел в квадрат в качестве опорного числа можно использовать любое. Тогда при одинаковой чётности сомножителей опорное число можно выбрать ровно посередине между ними. В этом случае сомножители равноудалены от опорного числа и произведение вычисляется по формуле разности квадратов.

24 ⋅ 28 = 26² − 2² = 676 − 4 = 672

37 ⋅ 39 = 38² − 1² = 1444 − 1 = 1443

83 ⋅ 89 = 86² − 3² = 7396 − 9 = 7387

72 ⋅ 92 = 82² − 10² = 6724 − 100 = 6624

Частные случаи

Изложенные ранее способы быстрого умножения вытекают из метода опорного числа при частных значениях N, a и b

Перемножение чисел от 11 до 19: N = 10
Возведение чисел в квадрат: a = b, A и B находятся по одну сторону от N
Перемножение чисел, сумма единиц которых равна 10: a + b = 10
Перемножение чисел, равноудалённых от круглого числа: a = b, A и B находятся по разные стороны от N

Перемножение произвольных чисел

Лёгкость применения метода опорного числа зависит от близости сомножителей к опорному числу, а значит и друг к другу. Если сомножители сильно отличаются и больший сомножитель является составным числом, можно приблизить его к меньшему сомножителю путём деления на некоторое число n, произвести умножение методом опорного числа и умножить результат на n.

88 ⋅ 23 = 4 ⋅ 22 ⋅ 23 = 4 ⋅ 506 = 2034

Когда больший сомножитель является простым числом, можно приблизить к нему меньший сомножитель путём умножения на некоторое число n, произвести умножение методом опорного числа и результат разделить на n.

31 ⋅ 87 = ¹⁄₃ ⋅ 93 ⋅ 87 = ¹⁄₃ ⋅ (8100 − 9) = 2700 − 3 = 2697

В общем случае, при перемножении сильно различающихся чисел, проще использовать способ умножения "крестом".

Перемножение чисел "крестом"

Умножение двузначных чисел

Общее правило

Перемножим два двузначных числа nm и pq

nm ⋅ pq = (10 ⋅ n + m) × (10 ⋅ p + q) = 100 ⋅ n ⋅ p + 10 ⋅ (n ⋅ q + m ⋅ p) + m ⋅ q

Таким образом

nm ⋅ pq = (n ⋅ p) ⋅ 100 + (m ⋅ p + n ⋅ q) ⋅ 10 + m ⋅ q

Правило умножения двузначных чисел крестом

Количества десятков перемножаются и дают количество сотен (приписывается два нуля) искомого произведения
Количества десятков перемножаются крест-накрест с количествами единиц, сумма этих двух произведений даёт количество десятков (приписывается ноль) искомого произведения
Количества единиц перемножаются и дают количество единиц искомого произведения

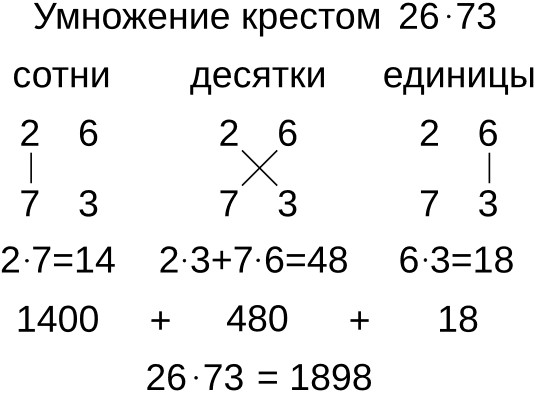
Примеры применения правила

47 ⋅ 89 = (4 ⋅ 8) ⋅ 100 + (7 ⋅ 8 + 4 ⋅ 9) ⋅ 10 + 7 ⋅ 9 = 3200 + 920 + 63 = 4183

34 ⋅ 85 = 2400 + (32 + 15) ⋅ 10 + 20 = 2400 + 470 + 20 = 2890

58 ⋅ 23 = 1000 + (160 + 150) + 24 = 1334

Частные случаи

Наиболее просто пользоваться этим правилом, когда сомножители оканчиваются на 1

41 ⋅ 31 = 1200 + (40 + 30) + 1 = 1271

Когда сомножители начинаются или оканчиваются одинаковой цифрой, это тоже облегчает вычисление

34 ⋅ 84 = 2400 + (3 + 8) ⋅ 4 ⋅ 10 + 16 = 2856

72 ⋅ 76 = 4900 + 560 + 12 = 5472

Умножение трёхзначных чисел

Способ умножения "крестом" можно обобщить на перемножение трёхзначных чисел, но объём вычислений при этом существенно увеличивается.

Сумма членов последовательности

Числовая последовательность это множество, в котором

определён порядок следования элементов
каждый элемент множества является числом

Иначе говоря, числовая последовательность это упорядоченное множество чисел

Группировка слагаемых

При вычислении суммы нескольких чисел можно воспользоваться перестановочным свойством сложения и объединить слагаемые, сумма которых является круглым числом. Круглые числа складывать легче.

12 + 9 + 14 + 18 + 11 = (12 + 18) + (9 + 11) + 14 = 30 + 20 + 14 = 50 + 14 = 64

Аналогичный способ применяется при вычислении произведения нескольких чисел. В этом случае используется перестановочное свойство умножения и объединяются множители, произведение которых является круглым числом. Круглые числа умножать легче.

5 ⋅ 7 ⋅ 12 = (5 ⋅ 12) ⋅ 7 = 60 ⋅ 7 = 420

15 ⋅ 9 ⋅ 6 = (15 ⋅ 6) ⋅ 9 = 90 ⋅ 9 = 810

Поразрядное сложение

Если в сумме отсутствуют слагаемые, которые дают круглые числа при сложении, можно из каждого слагаемого выделить количества десятков и единиц, группировать по разрядам. Десятки складываются с десятками, единицы — с единицами.

36 + 52 + 87 + 41 = (30 + 50 + 80 + 40) + (6 + 2 + 7 + 1) = 200 + 16 = 216

Данный способ представляется в виде формулы

na + mb + … + kc = n0 + m0 + … + k0 + a + b + … + c

Использование среднего числа

Если в сумму входят близкие по значению числа, можно выделить из них среднее число и каждое слагаемое в сумме представить в виде суммы среднего числа и поправки. В таком случае нахождение суммы сводится к умножению количества слагаемых на среднее число и сложению поправок.

73 + 65 + 72 + 69 + 68 + 71 = 6 ⋅ 70 + 3 − 5 + 2 − 1 − 2 + 1 = 420 − 2 = 418

Такие суммы встречаются при обработке результатов измерений или учёта, когда числовые данные случайным образом распределены возле некоторого среднего значения.

A₁ + A₂ + … + A_n = (A + a₁) + (A − a₂) + … + (A + a_n) = n ⋅ A + a₁ − a₂ + … + a_n

Здесь A — среднее чисел A₁, A₂, … , A_n; a₁, a₂, … , a_n — дополнения этих чисел до A.

Сумма членов арифметической прогрессии

Арифметическая прогрессия это числовая последовательность, в которой каждый последующий член отличается от предыдущего на одно и то же число. Это число называется разностью арифметической прогрессии.

Рассмотрим следующую сумму членов арифметической прогрессии

5 + 10 + 15 + … + 40 + 45 + 50

Можно заметить, что сумма членов, равноудалённых от концов выражения, одинакова

5 + 50 = 55, 10 + 45 = 55, 15 + 40 = 55, …

Количество членов, входящих в данную сумму, является чётным, поэтому для каждого члена имеется парный, находящийся на том же расстоянии от другого конца суммы. Количество пар в два раза меньше количества членов, входящих в сумму: 10 : 2 = 5. Таким образом, данная сумма равна 5 ⋅ 55 = 275.

Если количество членов, входящих в сумму, нечётно, то для центрального члена отсутствует пара. В таком случае находится сумма без центрального члена описанным выше способом, и к ней прибавляется центральный член.

Найдём сумму всех нечётных чисел от 50 до 100: 51 + 53 + … + 99. В эту сумму входят нечётные числа пяти полных десятков, в каждом десятке по пять нечётных чисел, следовательно количество членов, входящих в сумму, 5 ⋅ 5 = 25. Центральный член без пары это число 75. Количество пар членов, равноудалённых от концов, равно 24 : 2 = 12, сумма каждой пары 51 + 99 = 150.

51 + 53 + … + 75 + … + 97 + 99 = 12 ⋅ 150 + 75 = 1875

Пособия по устному счёту

[1] С.А.Рачинский. 1001 задача для умственного счёта (1897) — задачи на устный счёт

[2] Билл Хэндли. Считайте в уме как компьютер (2006) — метод опорного числа

https://www.youtube.com/watch?v=y7fcb-WFuUA
Видеозапись выступления счётчика Игоря Шелушкова — фрагмент из фильма "7 шагов за горизонт" 1968 года (СССР)

Размещено на сайте 15.01.2021
Дополнено 07.07.2022

УСЛОВИЯ КОПИРОВАНИЯ